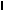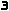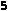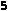Em juros compostos, o problema principal consiste em calcular o montante (soma) S obtido pela aplicação de um único valor principal P no instante t=0, à taxa i de juros (por período) durante n períodos.
Exemplo preparatório: Consideremos uma situação hipotética que, em 1994 a correção da caderneta de poupança tenha sido de 50% em cada um dos 5 primeiros meses do ano. Se uma pessoa depositou $100,00 em 01/01/94, poderiamos montar uma tabela para obter o resultado acumulado em 01/06/94.
|
Tempo
|
Data
|
Valor Principal
|
Juros
|
Montante
|
|
0
|
01/01/94
|
100,00
|
0
|
100,00
|
|
1
|
01/02/94
|
100,00
|
50,00
|
150,00
|
|
2
|
01/03/94
|
150,00
|
75,00
|
225,00
|
|
3
|
01/04/94
|
225,00
|
112,50
|
337,50
|
|
4
|
01/05/94
|
337,50
|
168,75
|
506,20
|
|
5
|
01/06/94
|
506,25
|
253,13
|
759,38
|
Observamos que os juros foram calculados sobre os Principais nos inícios dos meses que correspondiam aos montantes dos finais dos meses anteriores.
Juros Compostos são juros sobre juros (anatocismo)
A situação apresentada acima, pode ser analisada do ponto de vista matemático, com P=100,00 e i=50%=0,5. Assim:
|
S1=100(1,5)1
|
S2=100(1,5)2
|
S3=100(1,5)3
|
S4=100(1,5)4
|
S5=100(1,5)5
|
Em geral:
onde
|
Sn
|
Soma ou montante
|
|
P
|
Valor Principal aplicado inicialmente
|
|
i
|
taxa unitária
|
|
n
|
número de períodos da aplicação
|
Observação: Relembramos que a taxa e o número de períodos devem ser compatíveis ou homogêneos com respeito à unidade de tempo.
A fórmula para o cálculo do Montante, em função do valor Principal P, da taxa i ao período e do número de períodos n, é dada por:
Exemplo: Se a taxa de uma aplicação é de 150% ao ano, quanto tempo será necessário para dobrar o capital aplicado através de capitalização composta?
Objetivo: S=2P
Taxa anual: i=150/100=1,5. A fórmula é dada por:
Solução: 2P=P(1+1,5)n, logo
Para resolver esta última equação, aplicamos logaritmos a ambos os lados da igualdade, para obter:
n = log(2) / log(2,5) = 0,7564708 de 1 ano